Basing The Results On Probability
Probability is the likelihood or chance of an event occurring.
For example, the probability of flipping a coin and information technology being heads is ½, because there is 1 mode of getting a head and the full number of possible outcomes is two (a caput or tail). We write P(heads) = ½ .
- The probability of something which is sure to happen is 1.
- The probability of something which is incommunicable to happen is 0.
- The probability of something not happening is ane minus the probability that it will happen.
This video is a guide to probability. Expressing probability as fractions and percentages based on the ratio of the number means an outcome tin happen and the full number of outcomes is explained. Experimental probability and the importance of basing this on a large trial is also covered.
Single Events
E xample
At that place are 6 beads in a purse, 3 are red, 2 are yellow and 1 is blue. What is the probability of picking a yellow?
The probability is the number of yellows in the pocketbook divided by the full number of balls, i.east. 2/half dozen = 1/3.
E xample
In that location is a bag full of coloured balls, crimson, blue, green and orange. Balls are picked out and replaced. John did this 1000 times and obtained the following results:
- Number of blue balls picked out: 300
- Number of cerise balls: 200
- Number of green balls: 450
- Number of orange assurance: l
a) What is the probability of picking a green ball?
For every one thousand balls picked out, 450 are green. Therefore P(light-green) = 450/grand = 0.45
b) If at that place are 100 assurance in the pocketbook, how many of them are likely to exist dark-green?
The experiment suggests that 450 out of 1000 balls are dark-green. Therefore, out of 100 balls, 45 are dark-green (using ratios).
Multiple Events
Contained and Dependent Events
Suppose now we consider the probability of ii events happening. For example, we might throw 2 dice and consider the probability that both are half dozen's.
Nosotros telephone call two events contained if the outcome of one of the events doesn't affect the effect of another. For example, if we throw two dice, the probability of getting a 6 on the second die is the same, no matter what we get with the offset i- it's still one/half dozen.
On the other hand, suppose we have a bag containing two red and 2 blueish balls. If we pick ii balls out of the bag, the probability that the second is blue depends upon what the colour of the get-go ball picked was. If the starting time brawl was blue, at that place will be 1 blue and two carmine assurance in the purse when we selection the second ball. Then the probability of getting a blueish is 1/three. However, if the first brawl was red, there volition be 1 red and 2 bluish assurance left so the probability the 2d ball is blue is 2/3. When the probability of one event depends on some other, the events are dependent .
Possibility Spaces
When working out what the probability of 2 things happening is, a probability/ possibility space can be drawn. For example, if you throw 2 dice, what is the probability that you lot will become: a) viii, b) 9, c) either eight or nine?
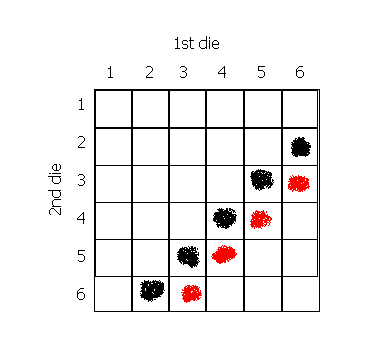
a) The blackness blobs indicate the ways of getting 8 (a 2 and a 6, a 3 and a 5, ...). In that location are v different ways. The probability infinite shows us that when throwing two dice, there are 36 dissimilar possibilities (36 squares). With 5 of these possibilities, yous will get 8. Therefore P(eight) = 5/36 .
b) The red blobs betoken the ways of getting 9. There are four ways, therefore P(nine) = 4/36 = 1/ix.
c) You will get an viii or 9 in any of the 'blobbed' squares. There are 9 birthday, so P(8 or ix) = 9/36 = 1/four .
Probability Copse
Another mode of representing 2 or more events is on a probability tree.
Eastward xample
There are 3 balls in a pocketbook: red, xanthous and blue. One ball is picked out, and not replaced, and then another ball is picked out.
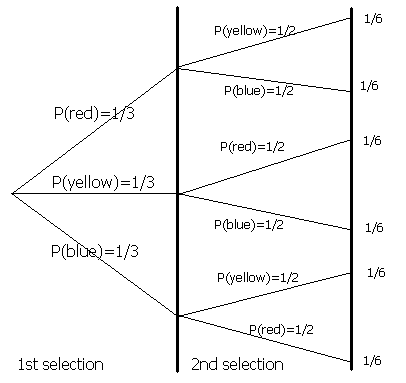
The start ball can exist red, yellowish or blueish. The probability is i/iii for each of these. If a red brawl is picked out, at that place will exist 2 balls left, a yellow and blue. The probability the second ball will be xanthous is 1/ii and the probability the second ball will be blue is 1/two. The same logic tin can be practical to the cases of when a yellowish or blue ball is picked out first.
In this instance, the question states that the ball is not replaced. If it was, the probability of picking a reddish ball (etc.) the 2nd fourth dimension will exist the aforementioned as the commencement (i.e. 1/3).
This video shows examples of using probability trees to work out the overall probability of a series of events are shown. Both independent and provisional probability are covered.
The AND and OR rules (HIGHER TIER)
In the above example, the probability of picking a ruby first is 1/3 and a yellowish 2d is ane/2. The probability that a red And then a yellow will be picked is i/three × 1/2 = 1/6 (this is shown at the cease of the co-operative). The rule is:
- If ii events A and B are independent (this ways that one outcome does not depend on the other), then the probability of both A and B occurring is establish by multiplying the probability of A occurring by the probability of B occurring.
The probability of picking a red OR yellow offset is one/3 + 1/3 = ii/3. The rule is:
- If we have two events A and B and it isn't possible for both events to occur, then the probability of A or B occuring is the probability of A occurring + the probability of B occurring.
On a probability tree, when moving from left to right nosotros multiply and when moving downwardly we add.
E xample
What is the probability of getting a yellow and a red in any guild?
This is the same as: what is the probability of getting a xanthous AND a carmine OR a red AND a yellowish.
P(xanthous and crimson) = 1/3 × i/2 = i/6
P(red and yellow) = 1/3 × 1/2 = 1/half-dozen
P(yellow and reddish or red and xanthous) = i/6 + 1/half-dozen = 1/3
Basing The Results On Probability,
Source: https://revisionmaths.com/gcse-maths-revision/statistics-handling-data/probability
Posted by: harrisfroplithe.blogspot.com


0 Response to "Basing The Results On Probability"
Post a Comment